Taiwan Election Data
[1] "District" "Sex" "Age" "Edu"
[5] "Arear" "Career" "Career8" "Ethnic"
[9] "Party" "PartyID" "Tondu" "Tondu3"
[13] "nI2" "votetsai" "green" "votetsai_nm"
[17] "votetsai_all" "Independence" "Unification" "sq"
[21] "Taiwanese" "edu" "female" "whitecollar"
[25] "lowincome" "income" "income_nm" "age"
[29] "KMT" "DPP" "npp" "noparty"
[33] "pfp" "South" "north" "Minnan_father"
[37] "Mainland_father" "Econ_worse" "Inequality" "inequality5"
[41] "econworse5" "Govt_for_public" "pubwelf5" "Govt_dont_care"
[45] "highincome" "votekmt" "votekmt_nm" "Blue"
[49] "Green" "No_Party" "voteblue" "voteblue_nm"
[53] "votedpp_1" "votekmt_1"
Call:
glm(formula = votetsai ~ female, family = binomial, data = TEDS_2016)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.4180 -1.3889 0.9546 0.9797 0.9797
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.54971 0.08245 6.667 2.61e-11 ***
female -0.06517 0.11644 -0.560 0.576
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1666.5 on 1260 degrees of freedom
Residual deviance: 1666.2 on 1259 degrees of freedom
(429 observations deleted due to missingness)
AIC: 1670.2
Number of Fisher Scoring iterations: 4
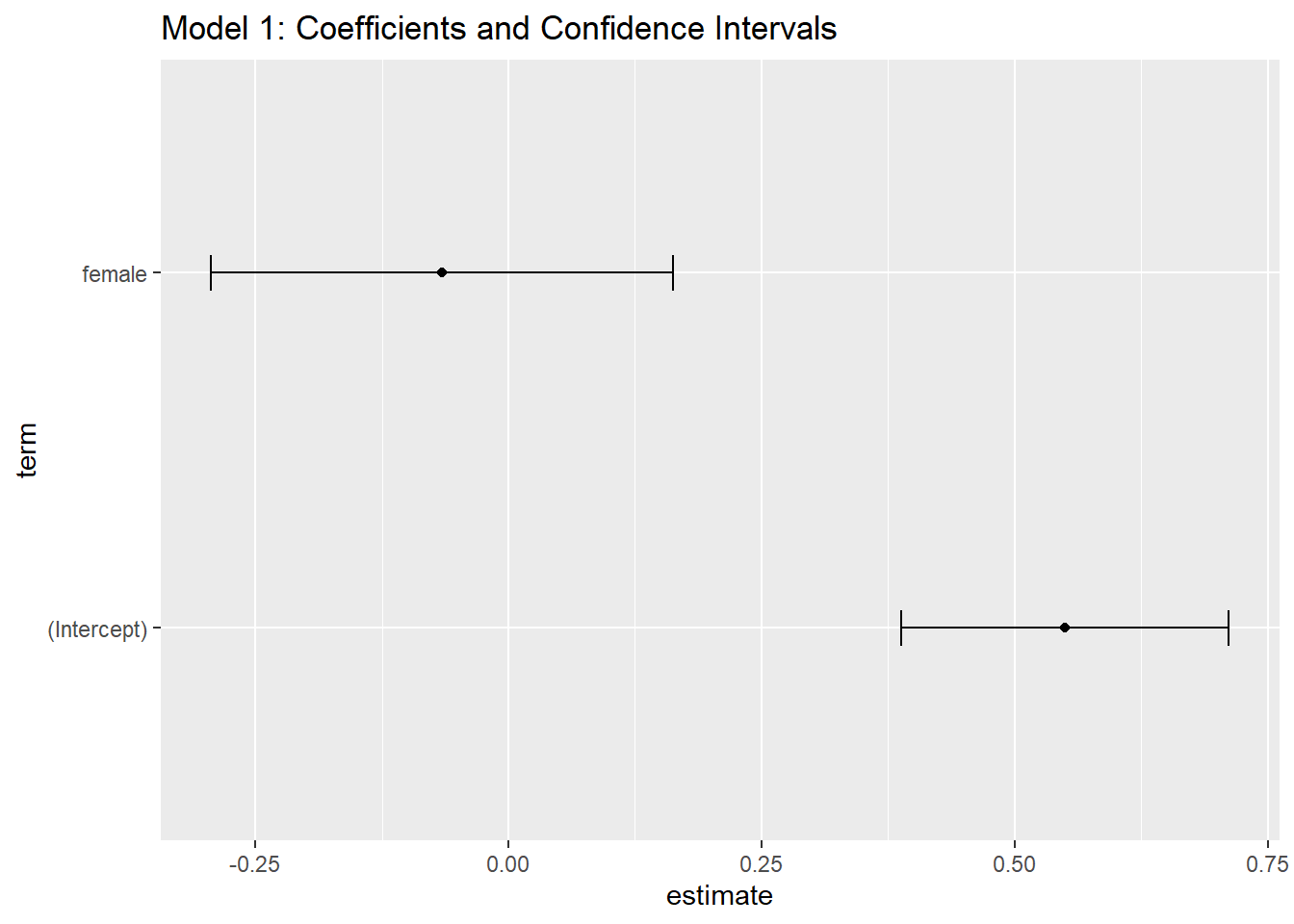
Interpreting the first logistic regression model
Based on the output of the logistic regression model, the coefficient for the female variable is -0.06517, and the p-value is 0.576. Since the p-value is greater than the standard significance level of 0.05, we fail to reject the null hypothesis, and there is no evidence to suggest that female voters are more likely to vote for President Tsai than male voters in this model.
The intercept of the model is 0.54971, which represents the log-odds of votetsai (voting for Tsai Ing-wen) for the reference group (male voters) in this case. The negative coefficient for the female variable (-0.06517) indicates that the log-odds of votetsai for female voters are slightly lower than for male voters, but this difference is not statistically significant.
It is essential to note that this model only includes the female predictor variable. Adding more variables (e.g., party ID, demographics, or issue-specific variables) may improve the model and provide more insights into factors affecting voting for President Tsai, which is what the next section will attempt to do.
Call:
glm(formula = votetsai ~ female + KMT + DPP + age + edu + income,
family = binomial, data = TEDS_2016)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.7360 -0.3673 0.2408 0.2946 2.5408
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.618640 0.592084 2.734 0.00626 **
female 0.047406 0.177403 0.267 0.78930
KMT -3.156273 0.250360 -12.607 < 2e-16 ***
DPP 2.888943 0.267968 10.781 < 2e-16 ***
age -0.011808 0.007164 -1.648 0.09931 .
edu -0.184604 0.083102 -2.221 0.02632 *
income 0.013727 0.034382 0.399 0.68971
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1661.76 on 1256 degrees of freedom
Residual deviance: 836.15 on 1250 degrees of freedom
(433 observations deleted due to missingness)
AIC: 850.15
Number of Fisher Scoring iterations: 6
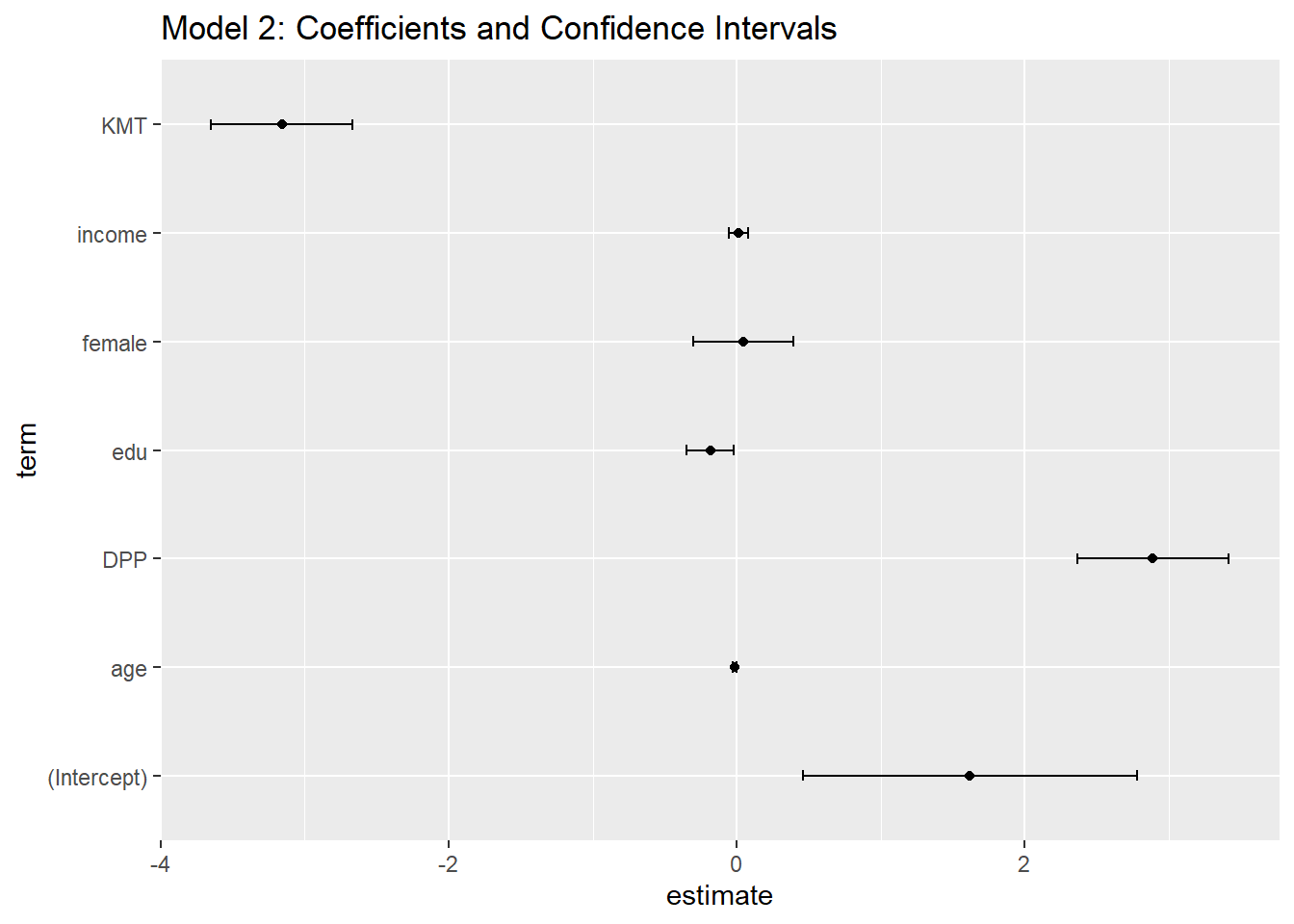
Interpretation for the updated model
Based on the output of the logistic regression model with additional predictors, here is the interpretation of the results:
Female: The coefficient for the female variable is 0.047406 with a p-value of 0.78930. The p-value is greater than 0.05, so the effect of the female variable is not statistically significant. This means that there is no evidence to suggest that female voters are more likely to vote for President Tsai compared to male voters, after controlling for other variables.
KMT: The coefficient for the KMT variable is -3.156273 with a p-value close to 0 (p < 2e-16). This indicates that respondents with a stronger KMT party affiliation are significantly less likely to vote for President Tsai.
DPP: The coefficient for the DPP variable is 2.888943 with a p-value close to 0 (p < 2e-16). This suggests that respondents with a stronger DPP party affiliation are significantly more likely to vote for President Tsai.
Age: The coefficient for the age variable is -0.011808 with a p-value of 0.09931. The p-value is slightly greater than 0.05, so the effect of age is not statistically significant at the 0.05 level. However, the negative coefficient suggests that older respondents are somewhat less likely to vote for President Tsai, but this relationship is weak.
Edu: The coefficient for the edu variable is -0.184604 with a p-value of 0.02632. The negative coefficient indicates that respondents with higher education levels are more likely to vote for President Tsai, and this effect is statistically significant (p < 0.05).
Income: The coefficient for the income variable is 0.013727 with a p-value of 0.68971. The p-value is greater than 0.05, so the effect of income is not statistically significant. This means that there is no evidence to suggest that income levels significantly influence the likelihood of voting for President Tsai.
In summary, the most significant predictors in this model are KMT and DPP party affiliations, which have strong and statistically significant effects on the likelihood of voting for President Tsai. Education also has a significant effect, while the female, age, and income variables are not statistically significant in this model.
Coefficient plots for the two models
Start: AIC=793.13
votetsai ~ female + KMT + DPP + age + edu + income + Independence +
Econ_worse + Govt_dont_care + Minnan_father + Mainland_father +
Taiwanese
Df Deviance AIC
- Govt_dont_care 1 767.14 791.14
- age 1 767.31 791.31
- female 1 767.40 791.40
- income 1 767.49 791.49
- Minnan_father 1 768.09 792.09
- edu 1 768.18 792.18
<none> 767.13 793.13
- Econ_worse 1 769.82 793.82
- Mainland_father 1 774.99 798.99
- Independence 1 784.68 808.68
- Taiwanese 1 787.92 811.92
- DPP 1 884.02 908.02
- KMT 1 954.40 978.40
Step: AIC=791.14
votetsai ~ female + KMT + DPP + age + edu + income + Independence +
Econ_worse + Minnan_father + Mainland_father + Taiwanese
Df Deviance AIC
- age 1 767.32 789.32
- female 1 767.40 789.40
- income 1 767.49 789.49
- Minnan_father 1 768.11 790.11
- edu 1 768.18 790.18
<none> 767.14 791.14
- Econ_worse 1 769.84 791.84
+ Govt_dont_care 1 767.13 793.13
- Mainland_father 1 775.08 797.08
- Independence 1 784.68 806.68
- Taiwanese 1 787.92 809.92
- DPP 1 884.68 906.68
- KMT 1 954.41 976.41
Step: AIC=789.32
votetsai ~ female + KMT + DPP + edu + income + Independence +
Econ_worse + Minnan_father + Mainland_father + Taiwanese
Df Deviance AIC
- female 1 767.59 787.59
- income 1 767.70 787.70
- Minnan_father 1 768.21 788.21
<none> 767.32 789.32
- Econ_worse 1 770.11 790.11
- edu 1 770.33 790.33
+ age 1 767.14 791.14
+ Govt_dont_care 1 767.31 791.31
- Mainland_father 1 775.09 795.09
- Independence 1 784.72 804.72
- Taiwanese 1 787.93 807.93
- DPP 1 885.39 905.39
- KMT 1 954.61 974.61
Step: AIC=787.59
votetsai ~ KMT + DPP + edu + income + Independence + Econ_worse +
Minnan_father + Mainland_father + Taiwanese
Df Deviance AIC
- income 1 767.95 785.95
- Minnan_father 1 768.49 786.49
<none> 767.59 787.59
- edu 1 770.43 788.43
- Econ_worse 1 770.44 788.44
+ female 1 767.32 789.32
+ age 1 767.40 789.40
+ Govt_dont_care 1 767.58 789.58
- Mainland_father 1 775.21 793.21
- Independence 1 785.27 803.27
- Taiwanese 1 787.94 805.94
- DPP 1 886.58 904.58
- KMT 1 955.77 973.77
Step: AIC=785.95
votetsai ~ KMT + DPP + edu + Independence + Econ_worse + Minnan_father +
Mainland_father + Taiwanese
Df Deviance AIC
- Minnan_father 1 768.87 784.87
<none> 767.95 785.95
- edu 1 770.43 786.43
- Econ_worse 1 770.69 786.69
+ income 1 767.59 787.59
+ female 1 767.70 787.70
+ age 1 767.74 787.74
+ Govt_dont_care 1 767.95 787.95
- Mainland_father 1 775.59 791.59
- Independence 1 785.62 801.62
- Taiwanese 1 788.14 804.14
- DPP 1 888.19 904.19
- KMT 1 956.43 972.43
Step: AIC=784.87
votetsai ~ KMT + DPP + edu + Independence + Econ_worse + Mainland_father +
Taiwanese
Df Deviance AIC
<none> 768.87 784.87
- Econ_worse 1 771.48 785.48
- edu 1 771.59 785.59
+ Minnan_father 1 767.95 785.95
+ income 1 768.49 786.49
+ female 1 768.61 786.61
+ age 1 768.74 786.74
+ Govt_dont_care 1 768.86 786.86
- Mainland_father 1 775.96 789.96
- Independence 1 786.35 800.35
- Taiwanese 1 788.59 802.59
- DPP 1 888.66 902.66
- KMT 1 956.56 970.56
Call:
glm(formula = votetsai ~ KMT + DPP + edu + Independence + Econ_worse +
Mainland_father + Taiwanese, family = binomial, data = TEDS_2016)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.0043 -0.3074 0.1731 0.4096 2.7622
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.05688 0.27971 0.203 0.83886
KMT -2.88317 0.25561 -11.280 < 2e-16 ***
DPP 2.47837 0.27407 9.043 < 2e-16 ***
edu -0.10296 0.06257 -1.645 0.09989 .
Independence 1.00339 0.24761 4.052 5.07e-05 ***
Econ_worse 0.30187 0.18640 1.619 0.10535
Mainland_father -0.85644 0.33052 -2.591 0.00956 **
Taiwanese 0.86729 0.19455 4.458 8.28e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1661.76 on 1256 degrees of freedom
Residual deviance: 768.87 on 1249 degrees of freedom
(433 observations deleted due to missingness)
AIC: 784.87
Number of Fisher Scoring iterations: 6
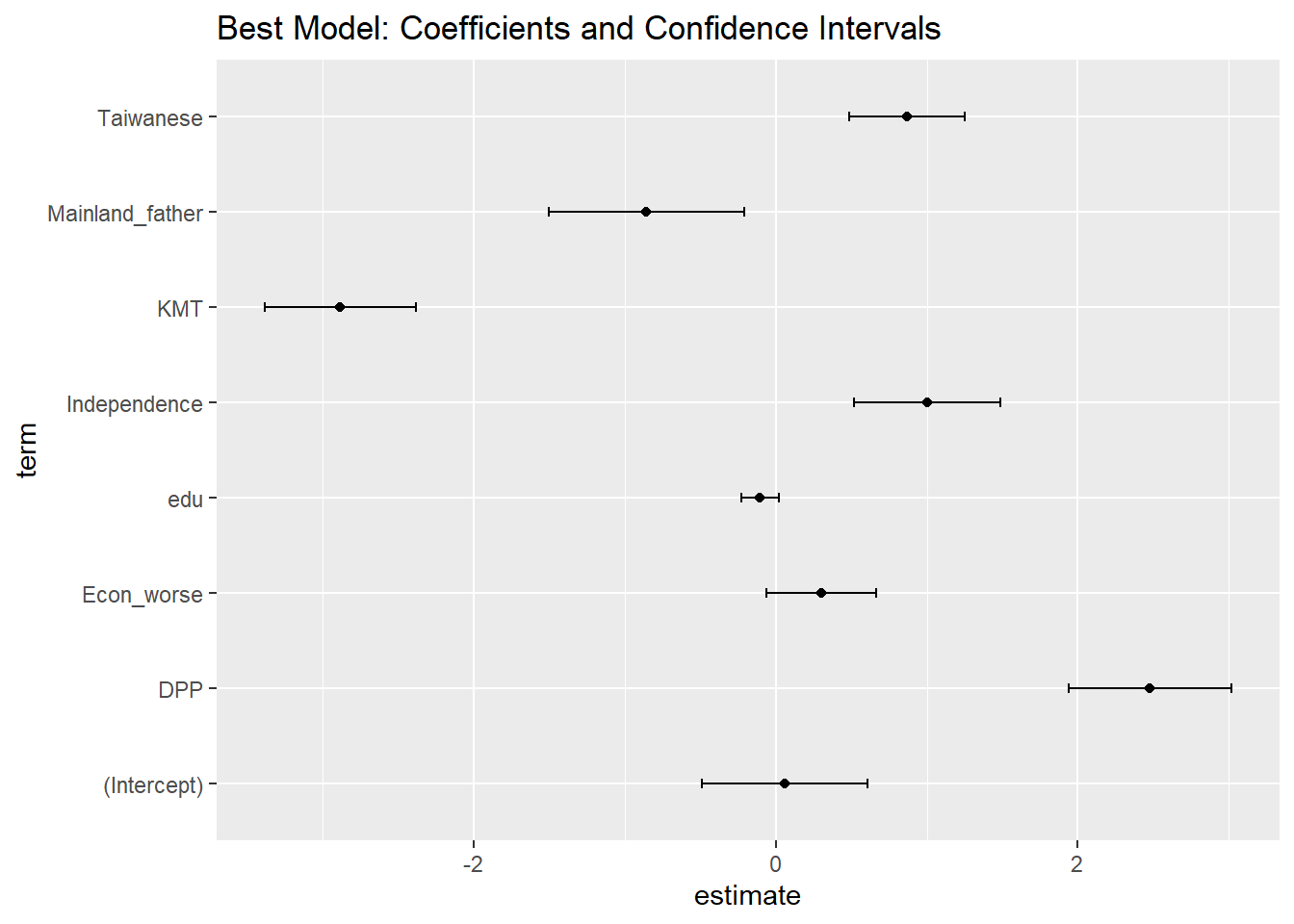
Interpreting the best model
This is the best model selected by stepAIC based on AIC criteria. The model predicts the likelihood of voting for Tsai Ing-wen (votetsai) using the following predictors: KMT, DPP, edu, Independence, Econ_worse, Mainland_father, and Taiwanese.
Here’s the interpretation of the model:
KMT (Kuomintang) Party ID: The coefficient is -2.88317, and it is highly significant (p < 2e-16). A one-unit increase in KMT affiliation is associated with a decrease in the log-odds of voting for Tsai Ing-wen by 2.88317 units, holding other variables constant. In other words, KMT supporters are less likely to vote for Tsai Ing-wen.
DPP (Democratic Progressive Party) Party ID: The coefficient is 2.47837, and it is highly significant (p < 2e-16). A one-unit increase in DPP affiliation is associated with an increase in the log-odds of voting for Tsai Ing-wen by 2.47837 units, holding other variables constant. DPP supporters are more likely to vote for Tsai Ing-wen.
Education (edu): The coefficient is -0.10296, and it is marginally significant (p = 0.09989). A one-unit increase in education level is associated with a decrease in the log-odds of voting for Tsai Ing-wen by 0.10296 units, holding other variables constant. More educated individuals are slightly less likely to vote for Tsai Ing-wen.
Independence: The coefficient is 1.00339, and it is highly significant (p = 5.07e-05). A one-unit increase in support for Taiwan’s independence is associated with an increase in the log-odds of voting for Tsai Ing-wen by 1.00339 units, holding other variables constant. Those who support Taiwan’s independence are more likely to vote for Tsai Ing-wen.
Economic evaluation (Econ_worse): The coefficient is 0.30187, and it is not significant (p = 0.10535). A one-unit increase in negative economic evaluation is associated with an increase in the log-odds of voting for Tsai Ing-wen by 0.30187 units, holding other variables constant. However, this effect is not statistically significant.
Mainland father (Mainland_father): The coefficient is -0.85644, and it is significant (p = 0.00956). A one-unit increase in being a descendent of mainland China is associated with a decrease in the log-odds of voting for Tsai Ing-wen by 0.85644 units, holding other variables constant. Individuals with mainland Chinese ancestry are less likely to vote for Tsai Ing-wen.
Self-identified Taiwanese (Taiwanese): The coefficient is 0.86729, and it is highly significant (p = 8.28e-06). A one-unit increase in self-identification as Taiwanese is associated with an increase in the log-odds of voting for Tsai Ing-wen by 0.86729 units, holding other variables constant. Self-identified Taiwanese are more likely to vote for Tsai Ing-wen.
The model has an AIC of 784.87, and the residual deviance is 768.87 on 1249 degrees of freedom. This model provides a better fit compared
Lab Assignment
[1] "crim" "zn" "indus" "chas" "nox" "rm" "age"
[8] "dis" "rad" "tax" "ptratio" "black" "lstat" "medv"
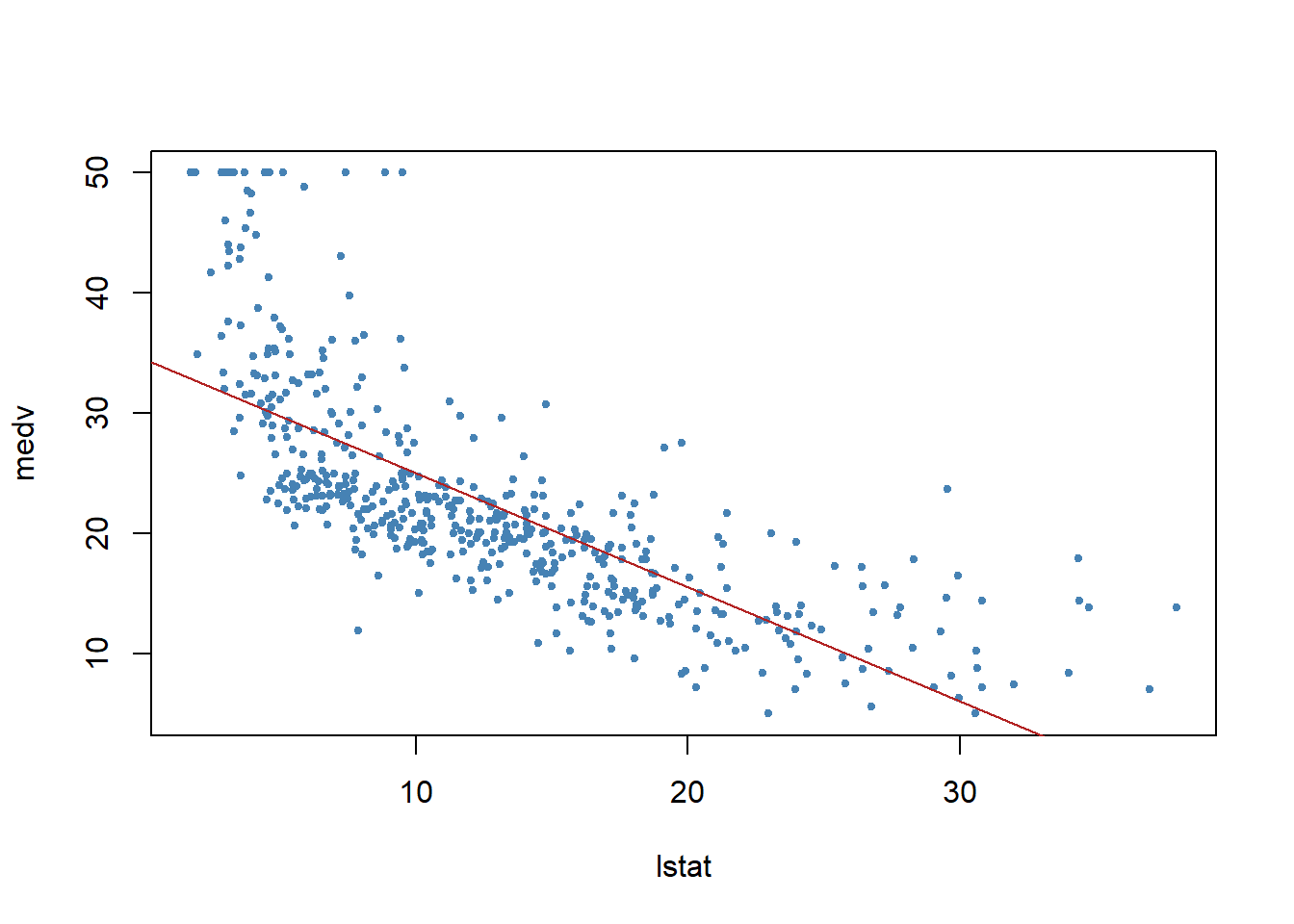
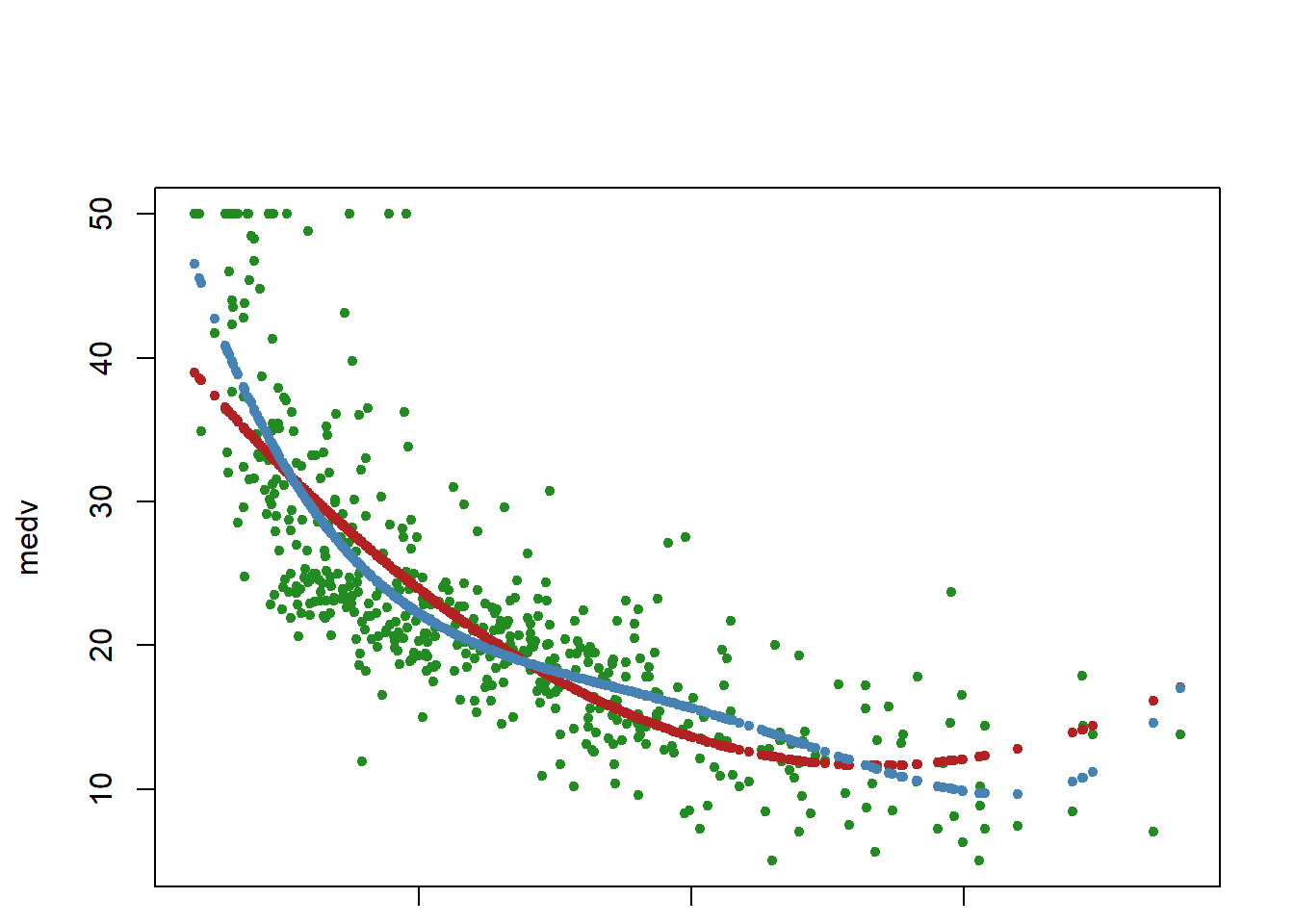
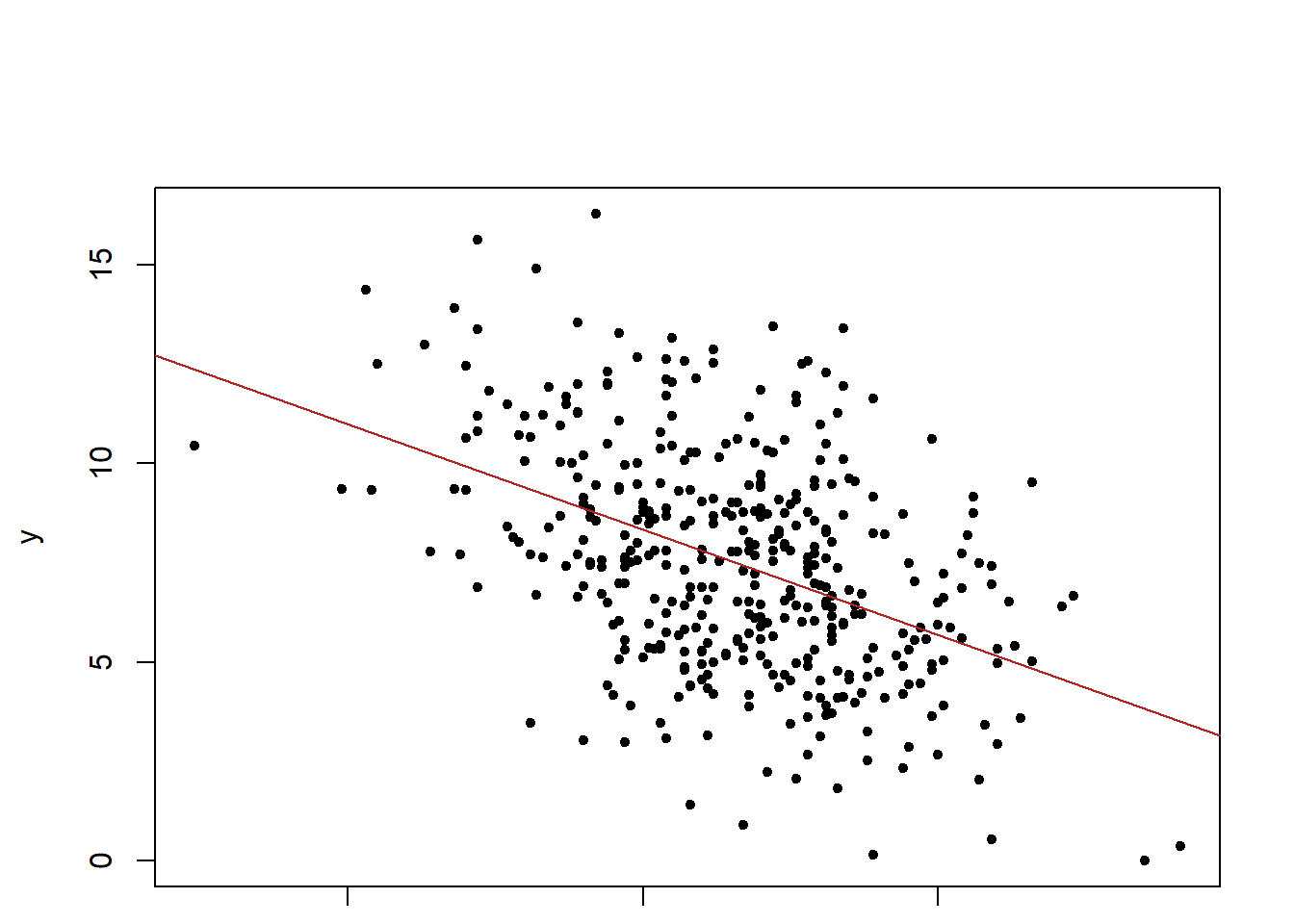
Call:
lm(formula = medv ~ lstat, data = Boston)
Coefficients:
(Intercept) lstat
34.55 -0.95
Call:
lm(formula = medv ~ lstat, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.168 -3.990 -1.318 2.034 24.500
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.55384 0.56263 61.41 <2e-16 ***
lstat -0.95005 0.03873 -24.53 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.216 on 504 degrees of freedom
Multiple R-squared: 0.5441, Adjusted R-squared: 0.5432
F-statistic: 601.6 on 1 and 504 DF, p-value: < 2.2e-16
[1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model"
2.5 % 97.5 %
(Intercept) 33.448457 35.6592247
lstat -1.026148 -0.8739505
fit lwr upr
1 34.55384 33.44846 35.65922
2 29.80359 29.00741 30.59978
3 25.05335 24.47413 25.63256
4 20.30310 19.73159 20.87461
fit lwr upr
1 34.55384 22.291923 46.81576
2 29.80359 17.565675 42.04151
3 25.05335 12.827626 37.27907
4 20.30310 8.077742 32.52846
Call:
lm(formula = medv ~ lstat + age, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.981 -3.978 -1.283 1.968 23.158
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 33.22276 0.73085 45.458 < 2e-16 ***
lstat -1.03207 0.04819 -21.416 < 2e-16 ***
age 0.03454 0.01223 2.826 0.00491 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.173 on 503 degrees of freedom
Multiple R-squared: 0.5513, Adjusted R-squared: 0.5495
F-statistic: 309 on 2 and 503 DF, p-value: < 2.2e-16
Call:
lm(formula = medv ~ ., data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.595 -2.730 -0.518 1.777 26.199
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.646e+01 5.103e+00 7.144 3.28e-12 ***
crim -1.080e-01 3.286e-02 -3.287 0.001087 **
zn 4.642e-02 1.373e-02 3.382 0.000778 ***
indus 2.056e-02 6.150e-02 0.334 0.738288
chas 2.687e+00 8.616e-01 3.118 0.001925 **
nox -1.777e+01 3.820e+00 -4.651 4.25e-06 ***
rm 3.810e+00 4.179e-01 9.116 < 2e-16 ***
age 6.922e-04 1.321e-02 0.052 0.958229
dis -1.476e+00 1.995e-01 -7.398 6.01e-13 ***
rad 3.060e-01 6.635e-02 4.613 5.07e-06 ***
tax -1.233e-02 3.760e-03 -3.280 0.001112 **
ptratio -9.527e-01 1.308e-01 -7.283 1.31e-12 ***
black 9.312e-03 2.686e-03 3.467 0.000573 ***
lstat -5.248e-01 5.072e-02 -10.347 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.745 on 492 degrees of freedom
Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
F-statistic: 108.1 on 13 and 492 DF, p-value: < 2.2e-16
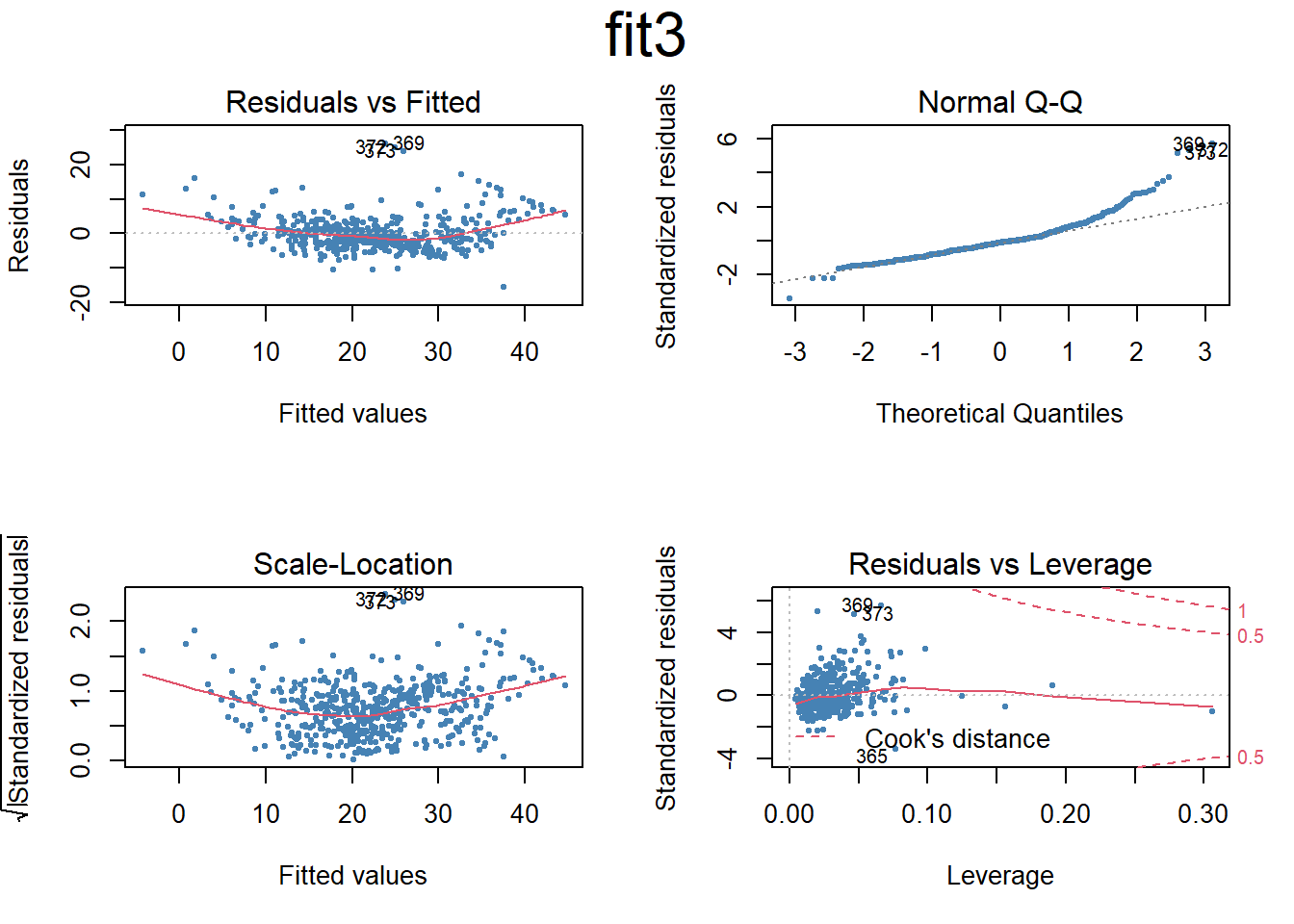
Call:
lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad +
tax + ptratio + black + lstat, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.5984 -2.7386 -0.5046 1.7273 26.2373
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.341145 5.067492 7.171 2.73e-12 ***
crim -0.108413 0.032779 -3.307 0.001010 **
zn 0.045845 0.013523 3.390 0.000754 ***
chas 2.718716 0.854240 3.183 0.001551 **
nox -17.376023 3.535243 -4.915 1.21e-06 ***
rm 3.801579 0.406316 9.356 < 2e-16 ***
dis -1.492711 0.185731 -8.037 6.84e-15 ***
rad 0.299608 0.063402 4.726 3.00e-06 ***
tax -0.011778 0.003372 -3.493 0.000521 ***
ptratio -0.946525 0.129066 -7.334 9.24e-13 ***
black 0.009291 0.002674 3.475 0.000557 ***
lstat -0.522553 0.047424 -11.019 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.736 on 494 degrees of freedom
Multiple R-squared: 0.7406, Adjusted R-squared: 0.7348
F-statistic: 128.2 on 11 and 494 DF, p-value: < 2.2e-16
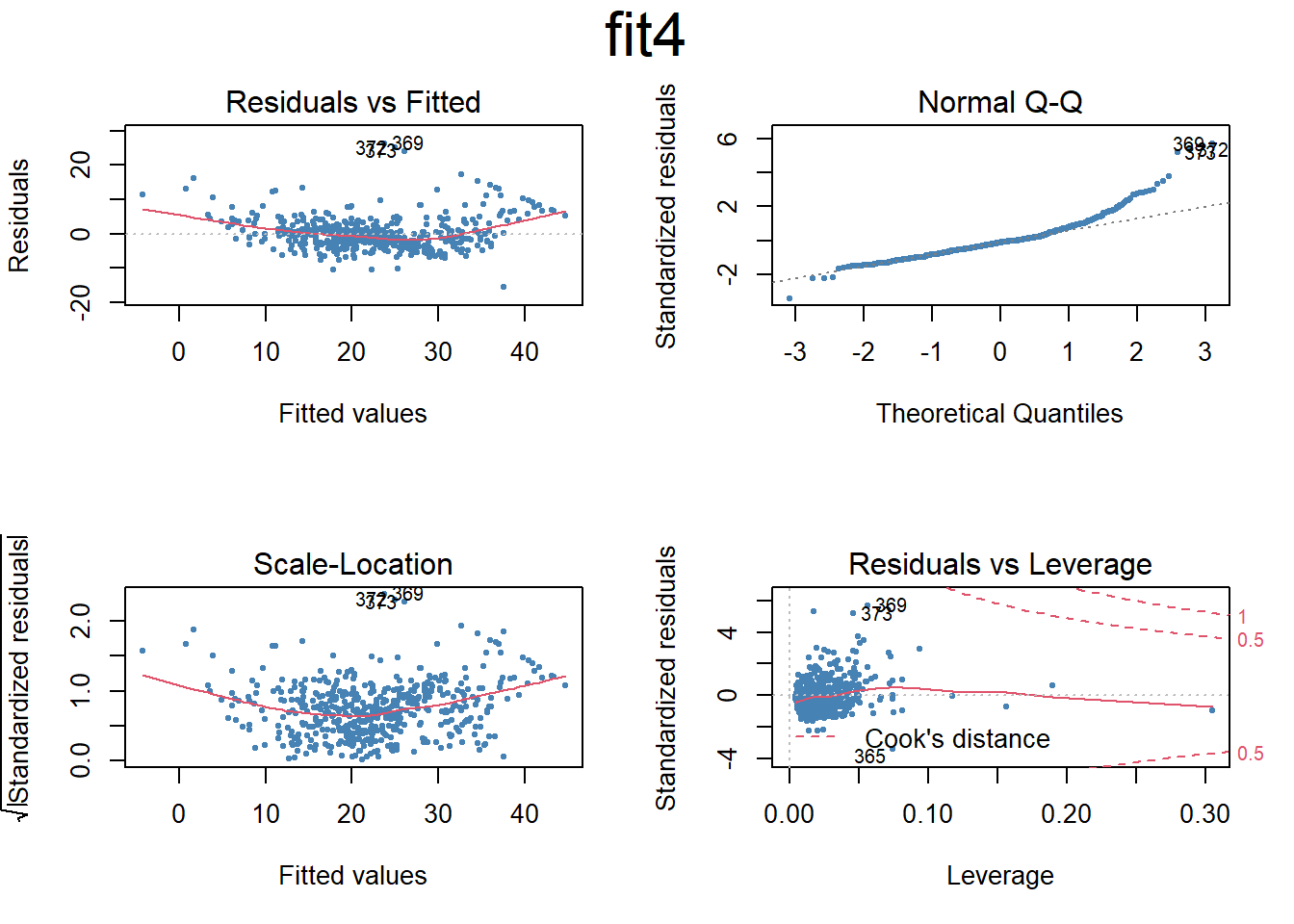
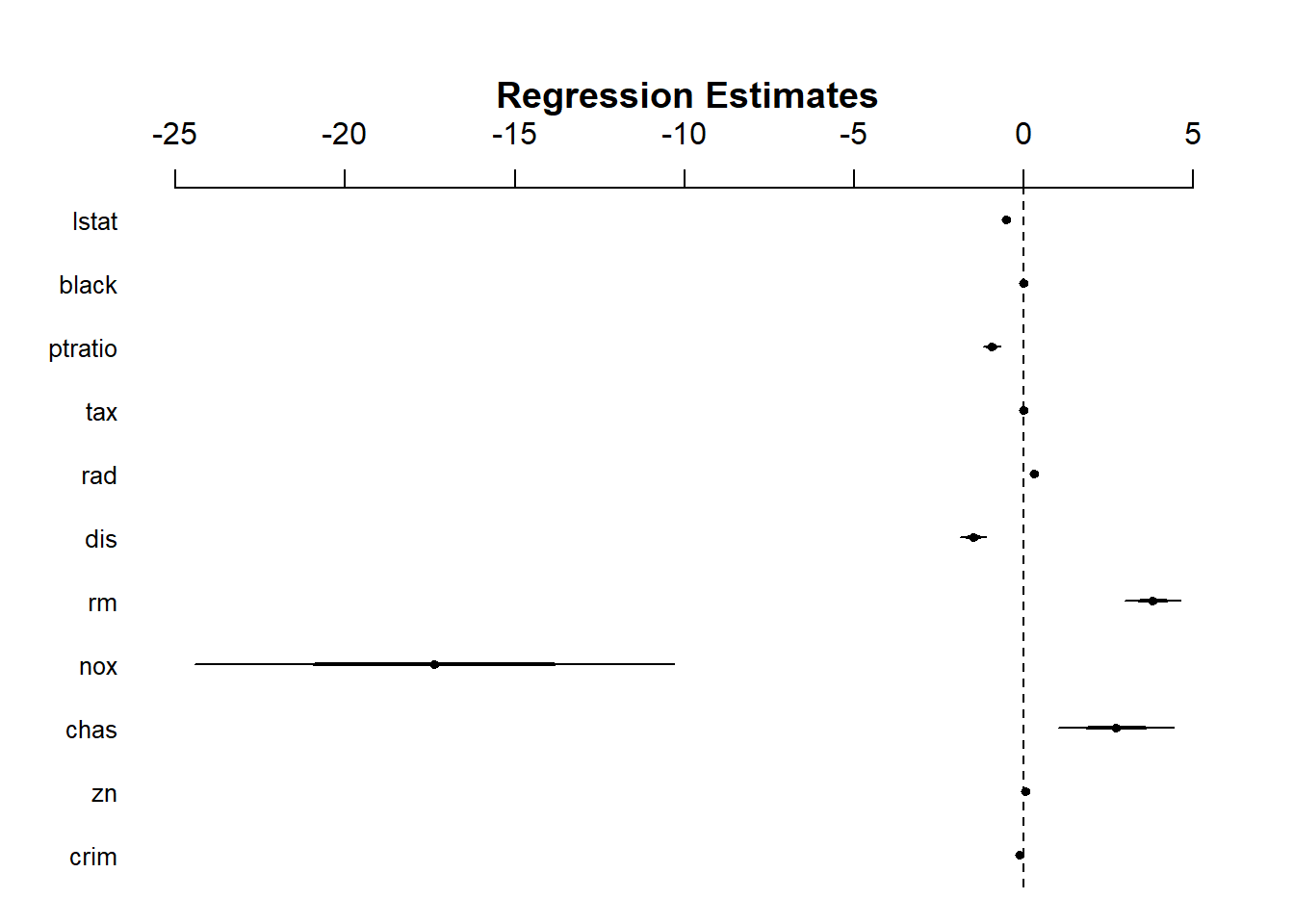
Call:
lm(formula = medv ~ lstat * age, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.806 -4.045 -1.333 2.085 27.552
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 36.0885359 1.4698355 24.553 < 2e-16 ***
lstat -1.3921168 0.1674555 -8.313 8.78e-16 ***
age -0.0007209 0.0198792 -0.036 0.9711
lstat:age 0.0041560 0.0018518 2.244 0.0252 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.149 on 502 degrees of freedom
Multiple R-squared: 0.5557, Adjusted R-squared: 0.5531
F-statistic: 209.3 on 3 and 502 DF, p-value: < 2.2e-16
Call:
lm(formula = medv ~ lstat + I(lstat^2), data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.2834 -3.8313 -0.5295 2.3095 25.4148
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.862007 0.872084 49.15 <2e-16 ***
lstat -2.332821 0.123803 -18.84 <2e-16 ***
I(lstat^2) 0.043547 0.003745 11.63 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 5.524 on 503 degrees of freedom
Multiple R-squared: 0.6407, Adjusted R-squared: 0.6393
F-statistic: 448.5 on 2 and 503 DF, p-value: < 2.2e-16
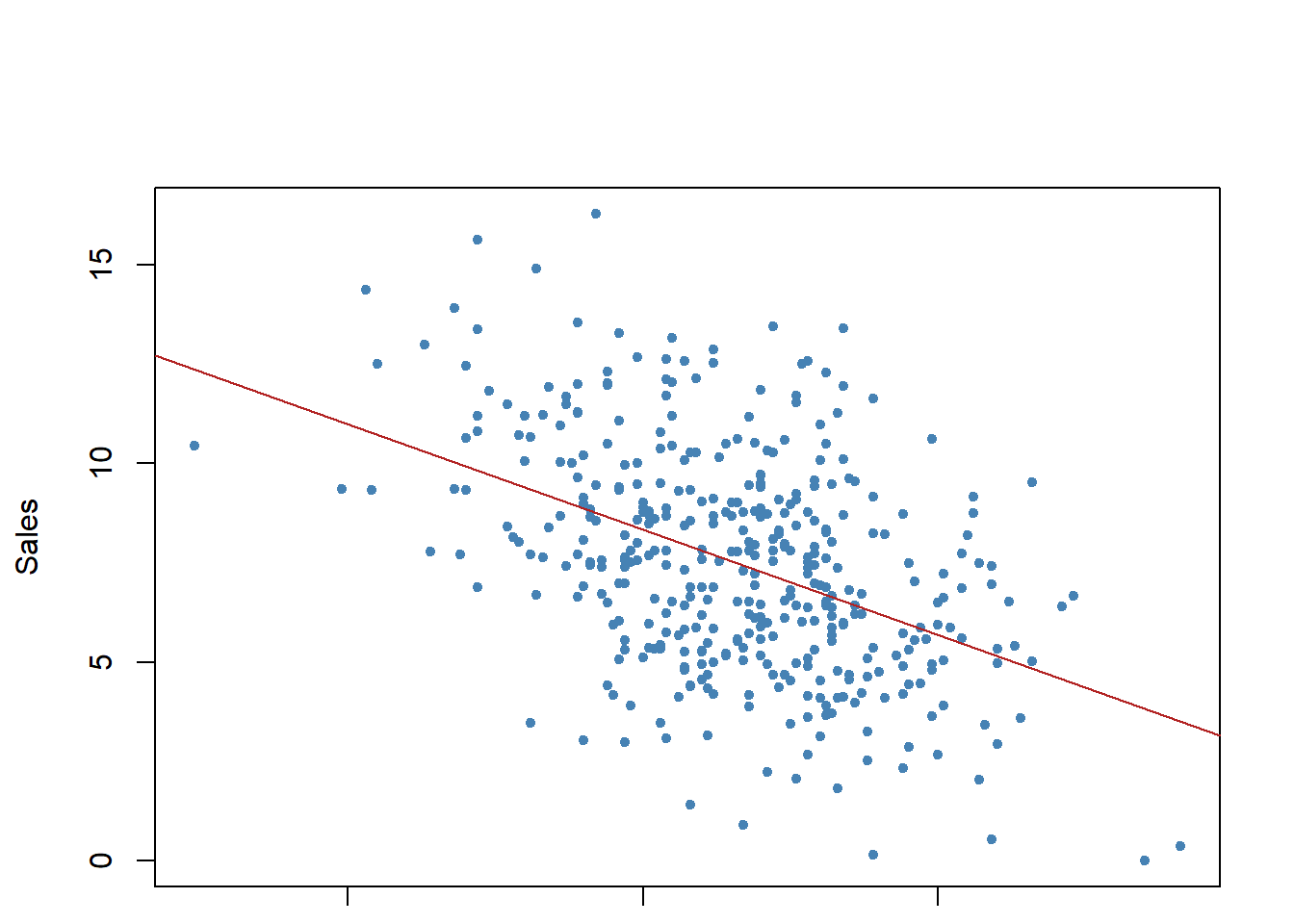
[1] "Sales" "CompPrice" "Income" "Advertising" "Population"
[6] "Price" "ShelveLoc" "Age" "Education" "Urban"
[11] "US"
Sales CompPrice Income Advertising
Min. : 0.000 Min. : 77 Min. : 21.00 Min. : 0.000
1st Qu.: 5.390 1st Qu.:115 1st Qu.: 42.75 1st Qu.: 0.000
Median : 7.490 Median :125 Median : 69.00 Median : 5.000
Mean : 7.496 Mean :125 Mean : 68.66 Mean : 6.635
3rd Qu.: 9.320 3rd Qu.:135 3rd Qu.: 91.00 3rd Qu.:12.000
Max. :16.270 Max. :175 Max. :120.00 Max. :29.000
Population Price ShelveLoc Age Education
Min. : 10.0 Min. : 24.0 Bad : 96 Min. :25.00 Min. :10.0
1st Qu.:139.0 1st Qu.:100.0 Good : 85 1st Qu.:39.75 1st Qu.:12.0
Median :272.0 Median :117.0 Medium:219 Median :54.50 Median :14.0
Mean :264.8 Mean :115.8 Mean :53.32 Mean :13.9
3rd Qu.:398.5 3rd Qu.:131.0 3rd Qu.:66.00 3rd Qu.:16.0
Max. :509.0 Max. :191.0 Max. :80.00 Max. :18.0
Urban US
No :118 No :142
Yes:282 Yes:258
Call:
lm(formula = Sales ~ . + Income:Advertising + Age:Price, data = Carseats)
Residuals:
Min 1Q Median 3Q Max
-2.9208 -0.7503 0.0177 0.6754 3.3413
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.5755654 1.0087470 6.519 2.22e-10 ***
CompPrice 0.0929371 0.0041183 22.567 < 2e-16 ***
Income 0.0108940 0.0026044 4.183 3.57e-05 ***
Advertising 0.0702462 0.0226091 3.107 0.002030 **
Population 0.0001592 0.0003679 0.433 0.665330
Price -0.1008064 0.0074399 -13.549 < 2e-16 ***
ShelveLocGood 4.8486762 0.1528378 31.724 < 2e-16 ***
ShelveLocMedium 1.9532620 0.1257682 15.531 < 2e-16 ***
Age -0.0579466 0.0159506 -3.633 0.000318 ***
Education -0.0208525 0.0196131 -1.063 0.288361
UrbanYes 0.1401597 0.1124019 1.247 0.213171
USYes -0.1575571 0.1489234 -1.058 0.290729
Income:Advertising 0.0007510 0.0002784 2.698 0.007290 **
Price:Age 0.0001068 0.0001333 0.801 0.423812
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.011 on 386 degrees of freedom
Multiple R-squared: 0.8761, Adjusted R-squared: 0.8719
F-statistic: 210 on 13 and 386 DF, p-value: < 2.2e-16
Good Medium
Bad 0 0
Good 1 0
Medium 0 1